MOVIMIENTO RECTILÍNEO UNIFORME

El Movimiento Rectilíneo
Uniforme es una trayectoria recta, su velocidad es constante y su aceleración es nula.
- Movimiento que se realiza sobre una línea recta.
- Velocidad constante; implica magnitud y dirección constantes.
- La magnitud de la velocidad recibe el nombre de aceleracion o rapidez.
- Aceleración nula.
La distancia recorrida se calcula multiplicando la magnitud de la velocidad media velocidad o rapidez por el tiempo transcurrido. Esta relación también es aplicable si la trayectoria no es rectilínea, con tal que la rapidez o módulo de la velocidad sea constante llamado movimiento de un cuerpo.
Al representar gráficamente la velocidad en función del tiempo se obtiene una recta paralela al eje de abscisas (tiempo). Además, el área bajo la recta producida representa la distancia recorrida.
La representación gráfica de la distancia recorrida en función del tiempo da lugar a una recta cuya pendiente se corresponde con la velocidad.
Por lo tanto el movimiento puede considerarse en dos sentidos; una velocidad negativa representa un movimiento en dirección contraria al sentido que convencionalmente hayamos adoptado como positivo.
las graficas tienen como nombre retilimatelero
De acuerdo con la Primera Ley de Newton, toda partícula permanece
en reposo o en movimiento rectilíneo uniforme cuando no hay una fuerza neta que
actúe sobre el cuerpo. Esta es una situación ideal, ya que siempre existen
fuerzas que tienden a alterar el movimiento de las partículas, por lo que en el
movimiento rectilíneo uniforme (M.R.U) es difícil encontrar la fuerza
amplificada, a tiempos iguales distancias iguales.
Movimiento rectilíneo
Se denomina movimiento rectilíneo, aquél cuya trayectoria es una línea recta.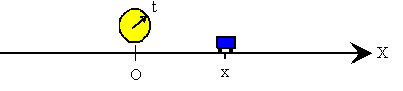
En la recta situamos un origen O, donde estará un observador que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen.
Posición
La posición x del móvil se puede relacionar con el tiempo t mediante una función x=f(t).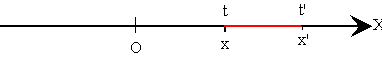
Desplazamiento
Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Dx=x'-x en el intervalo de tiempo Dt=t'-t, medido desde el instante t al instante t'.
Velocidad
La velocidad media entre los instantes t y t' está definida porPara determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Dt tan pequeño como sea posible, en el límite cuando Dt tiende a cero.
Pero dicho límite, es la definición de derivada de x con respecto del tiempo t.
GRAFICAS DE
MRU.
Al graficar el desplazamiento
(distancia) contra tiempo se obtiene ina línea recta. La pendiente de la línea
recta representa el valor de la velocidad para dicha partícula.
Al realizar la gráfica de velocidad
contra tiempo obtenemos una recta paralela al eje X. Podemos calcular el
deslazamiento como el área bajo la línea recta.
| ||||||||||
CAÍDA LIBRE
En física, se denomina caída
libre al movimiento de un cuerpo bajo la acción exclusiva de un campo
gravitatorio. Esta definición formal excluye a todas las caídas
reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar
en el seno de un fluido; sin embargo es
frecuente también referirse coloquialmente a éstas como caídas libres, aunque
los efectos de la viscosidad del
medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o a satélites no propulsados en órbita alrededor de la Tierra. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación alar ni de paracaídas durante un cierto trayecto.[1] [2]
En la física clásica, la fuerza gravitatoria que se ejerce sobre una masa es proporcional a la intensidad del campo gravitatorio en la posición espacial donde se encuentre dicha masa. La constante de proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como establece el principio de equivalencia. En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica. Por tanto, desde el punto de vista de la física clásica, un sistema de referencia en caída libre es un sistema acelerado por la fuerza de la gravedad y, como tal, es no inercial. Por el contrario, desde el punto de vista de la física relativista, el mismo sistema de referencia es inercial, pues aunque está acelerado en el espacio, no está acelerado en el espacio-tiempo. La diferencia radica en la propia definición de los conceptos geométricos y cinemáticos, que para cada marco teórico son completamente diferentes.
En la caída libre ideal, se desprecia la resistencia aerodinámica que
presenta el aire al movimiento del cuerpo, analizando lo que pasaría en el vacío. En esas condiciones, la
aceleración que adquiriría el cuerpo sería debida exclusivamente a la gravedad,
siendo independiente de su masa; por ejemplo, si dejáramos caer una bala de
cañón y una pluma en el vacío, ambos adquirirían la misma aceleración,  ,
que es la aceleración de la gravedad
,
que es la aceleración de la gravedad
 que actúa sobre un cuerpo es igual al producto de su masa
que actúa sobre un cuerpo es igual al producto de su masa  por la aceleración que adquiere. En caída libre sólo intervienen el peso
por la aceleración que adquiere. En caída libre sólo intervienen el peso 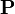 (vertical, hacia abajo) y el rozamiento aerodinámico
(vertical, hacia abajo) y el rozamiento aerodinámico 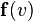 en
la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo
gravitatorio aproximadamente constante, la ecuación del movimiento de caída
libre es:
en
la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo
gravitatorio aproximadamente constante, la ecuación del movimiento de caída
libre es:
 lleva signo negativo porque se toma el eje vertical como positivo hacia
arriba.
lleva signo negativo porque se toma el eje vertical como positivo hacia
arriba.
El movimiento del cuerpo en caída libre es vertical con velocidad creciente
(aproximadamente movimiento uniformemente acelerado con aceleración g)
(aproximadamente porque la aceleración aumenta cuando el objeto disminuye en
altura, en la mayoría de los casos la variación es despreciable). La ecuación de
movimiento se puede escribir en términos la altura y:
 .
.
Si se integran las ecuaciones anteriores para el caso de caída libre desde una altura y
velocidad inicial nula y para el caso de lanzamiento vertical desde una altura
nula con una velocidad inicial
y
velocidad inicial nula y para el caso de lanzamiento vertical desde una altura
nula con una velocidad inicial 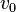 se
obtienen los siguientes resultados para la altura del cuerpo:
se
obtienen los siguientes resultados para la altura del cuerpo:
Caída libre ( y
y
 ):
):
 hasta la altura
hasta la altura 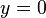 puede obtenerse al reordenar la ecuación anterior:
puede obtenerse al reordenar la ecuación anterior:
 y
y
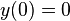 ):
):
 es
aquella en que la velocidad vertical se hace cero, entonces el tiempo
transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura
es
aquella en que la velocidad vertical se hace cero, entonces el tiempo
transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura
 puede calcularse como:
puede calcularse como:
 hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en
alcanzar la alura máxima de
hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en
alcanzar la alura máxima de  si
es lanzado desde el suelo. Para ello basta con probar la desigualdad
siguiente:
si
es lanzado desde el suelo. Para ello basta con probar la desigualdad
siguiente:
 y
que
y
que ![\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]](http://upload.wikimedia.org/math/2/a/8/2a8f254b20cdbb409d09efc8c1990a48.png)
Cuando un cuerpo cae en caída libre pero no parte del reposo porque tiene una
velocidad no nula, entonces la trayectoria de caída no es una recta sino una
curva aproximadamente parabólica. La ecuación de la
trayectoria en coordenadas cartesianas viene dada por:
donde x es la coordenada horizontal (eje de abcisas) e y la
coordenada vertical (eje de ordenadas).
La expresión de la velocidad vertical debe reescribirse en función de la coordenada x teniendo en cuenta que t = x/vx. Pueden distinguirse los siguientes casos:

El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o a satélites no propulsados en órbita alrededor de la Tierra. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación alar ni de paracaídas durante un cierto trayecto.[1] [2]
La caída libre como sistema de referencia
Un sistema de referencia ligado a un cuerpo en caída libre puede considerarse inercial o no inercial en función del marco teórico que esté utilizándose.En la física clásica, la fuerza gravitatoria que se ejerce sobre una masa es proporcional a la intensidad del campo gravitatorio en la posición espacial donde se encuentre dicha masa. La constante de proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como establece el principio de equivalencia. En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica. Por tanto, desde el punto de vista de la física clásica, un sistema de referencia en caída libre es un sistema acelerado por la fuerza de la gravedad y, como tal, es no inercial. Por el contrario, desde el punto de vista de la física relativista, el mismo sistema de referencia es inercial, pues aunque está acelerado en el espacio, no está acelerado en el espacio-tiempo. La diferencia radica en la propia definición de los conceptos geométricos y cinemáticos, que para cada marco teórico son completamente diferentes.
Caída libre ideal
 ,
que es la aceleración de la gravedad
,
que es la aceleración de la gravedadEcuación del movimiento
De acuerdo a la segunda ley de Newton, la fuerza que actúa sobre un cuerpo es igual al producto de su masa
que actúa sobre un cuerpo es igual al producto de su masa  por la aceleración que adquiere. En caída libre sólo intervienen el peso
por la aceleración que adquiere. En caída libre sólo intervienen el peso 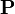 (vertical, hacia abajo) y el rozamiento aerodinámico
(vertical, hacia abajo) y el rozamiento aerodinámico 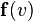 en
la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo
gravitatorio aproximadamente constante, la ecuación del movimiento de caída
libre es:
en
la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo
gravitatorio aproximadamente constante, la ecuación del movimiento de caída
libre es:La aceleración de la gravedad
 lleva signo negativo porque se toma el eje vertical como positivo hacia
arriba.
lleva signo negativo porque se toma el eje vertical como positivo hacia
arriba.Trayectoria en caída libre
- Caída libre
totalmente vertical
El movimiento del cuerpo en caída libre es vertical con velocidad creciente
(aproximadamente movimiento uniformemente acelerado con aceleración g)
(aproximadamente porque la aceleración aumenta cuando el objeto disminuye en
altura, en la mayoría de los casos la variación es despreciable). La ecuación de
movimiento se puede escribir en términos la altura y:(1)donde:
 ,
son la aceleración y la velocidad verticales.
,
son la aceleración y la velocidad verticales. ,
es la fuerza de rozamiento fluidodinámico (que aumenta con la
velocidad).
,
es la fuerza de rozamiento fluidodinámico (que aumenta con la
velocidad).
- Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuación diferencial () para las velocidades y la altura vienen dada por:
donde v0 es la velocidad inicial, para una caída desde el reposo v0 = 0 y h0 es la altura inicial de caída.
- Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la resistencia fluidodinámica que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico kw:
(2)En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial ():
Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:
- Un análisis más cuidadoso de la fricción de un fluido revelaría que a grandes velocidades el flujo alrededor de un objeto no puede considerarse laminar, sino turbulento y se producen remolinos alrededor del objeto que cae de tal manera que la fuerza de fricción se vuelve proporcional al cuadrado de la velocidad:
(3)Donde:
 ,
es el coeficiente aerodinámico de
resistencia al avance, que sólo depende de la forma del cuerpo.
,
es el coeficiente aerodinámico de
resistencia al avance, que sólo depende de la forma del cuerpo. ,
es el área transversal a la dirección del movimiento.
,
es el área transversal a la dirección del movimiento.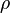 ,
es la densidad del fluido.
,
es la densidad del fluido.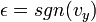 ,
es el signo de la velocidad.
,
es el signo de la velocidad.
La solución analítica de la ecuación diferencial () depende del signo relativo de la fuerza de rozamiento y el peso por lo que la solución analítica es diferente para un cuerpo que sube o para uno que cae. La solución de velocidades para ambos casos es:
Donde:
 .
.Si se integran las ecuaciones anteriores para el caso de caída libre desde una altura
 y
velocidad inicial nula y para el caso de lanzamiento vertical desde una altura
nula con una velocidad inicial
y
velocidad inicial nula y para el caso de lanzamiento vertical desde una altura
nula con una velocidad inicial 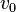 se
obtienen los siguientes resultados para la altura del cuerpo:
se
obtienen los siguientes resultados para la altura del cuerpo:Caída libre (
 y
y
 ):
):El tiempo transcurrido en la caída desde la altura
 hasta la altura
hasta la altura 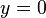 puede obtenerse al reordenar la ecuación anterior:
puede obtenerse al reordenar la ecuación anterior:Lanzamiento vertical (
 y
y
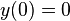 ):
):Si la altura
 es
aquella en que la velocidad vertical se hace cero, entonces el tiempo
transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura
es
aquella en que la velocidad vertical se hace cero, entonces el tiempo
transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura
 puede calcularse como:
puede calcularse como:Se puede demostrar que el tiempo que tarda un cuerpo en caer desde una altura
 hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en
alcanzar la alura máxima de
hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en
alcanzar la alura máxima de  si
es lanzado desde el suelo. Para ello basta con probar la desigualdad
siguiente:
si
es lanzado desde el suelo. Para ello basta con probar la desigualdad
siguiente:sabiendo que
 y
que
y
que ![\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]](http://upload.wikimedia.org/math/2/a/8/2a8f254b20cdbb409d09efc8c1990a48.png)
- Caída libre parabólica y casi-parabólica
Cuando un cuerpo cae en caída libre pero no parte del reposo porque tiene una
velocidad no nula, entonces la trayectoria de caída no es una recta sino una
curva aproximadamente parabólica. La ecuación de la
trayectoria en coordenadas cartesianas viene dada por:(4)
La expresión de la velocidad vertical debe reescribirse en función de la coordenada x teniendo en cuenta que t = x/vx. Pueden distinguirse los siguientes casos:
- Para un cuerpo en caída libre sin rozamiento, la trayectoria es exactamente una parábola dada por:
- Cuando se incluye el rozamiento aerodinámico, la trayectoria no es exactamente una parábola. Por ejemplo para una fuerza de rozamiento proporcional a la velocidad como en la () la trayectoria resulta ser:
Para una fuerza de rozamiento proporcional al cuadrado de la velocidad, la integración de las ecuaciones del movimiento es más compleja, presuponiendo fuerzas de rozamiento independientes en dirección horizontal y vertical proporcionales al cuadrado del valor de la componente:
La trayectoria viene dada por:
Las figuras adjuntas muestran la forma de las trayectorias para cinco valores diferentes del parámetro β para una misma altura de caída (medida en unidades de longitud δ).














![y(t)=h_0-\cfrac{1}{{\alpha}}\ln\left[\cosh\left(-t\sqrt{{\alpha}{g}}\right) \right]](http://upload.wikimedia.org/math/6/4/4/64407f2d5c666902f084e7350c123773.png)

![y(t)=\cfrac{1}{{\alpha}}\ln\left[\cfrac{\cos\left[-t\sqrt{{\alpha}{g}}+\arctan\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]}{\cos\left[\mbox{arctan}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]} \right]](http://upload.wikimedia.org/math/1/6/2/162a803c65007695a5634885c3c8cce0.png)




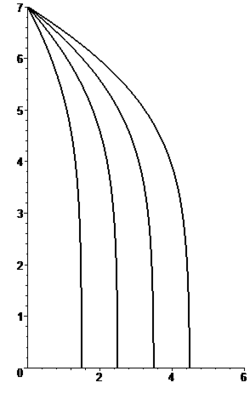
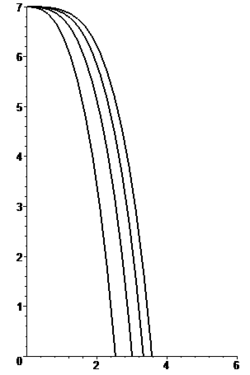

![y(x) = h_0 - \delta \left[\frac{x}{\beta\delta}-\ln \left(1-\frac{x}{\beta\delta} \right) \right] \qquad \begin{cases} \delta = gm^2/k_w^2\\ \beta = V_xk_w/mg\end{cases}](http://upload.wikimedia.org/math/2/4/9/2499cfce560492266eba090a5e021837.png)

![y(x) = h_0 - \delta \ln \left[\cosh \left( \frac{e^{x/\delta}-1}{\beta}\right) \right] \qquad \begin{cases} \delta = 1/C_w\\ \beta = \sqrt{g/(C_wV_x^2)} \end{cases}](http://upload.wikimedia.org/math/3/b/f/3bf3fe9845c590f97bd6f85495e3efd4.png)
No hay comentarios:
Publicar un comentario